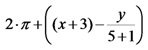[算法]遗传编程算法

转载;http://www.cnblogs.com/zgw21cn/archive/2009/11/07/1598238.html

假设从向银行申请贷款的顾户中，要选出优质顾客。怎么做？

现在有学习数据如下

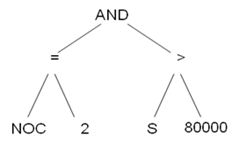
如果从学习数据中学习出如下规则

IF (孩子个数(NOC) = 2) AND (薪水(S) > 80000) THEN 优良顾客 ELSE 不良顾客。

这条规则以一条树的形式可以表现如下。

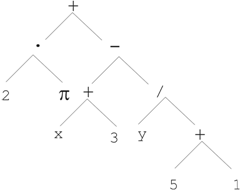
遗传编程(genetic programming)基于遗传算法，传统的遗传算法是用定长的线性字符串表示一个基因。而遗传编程基于树的形式，其树的深度和宽度是可变的。树可以轻易表达算术表达式，逻辑表达式，程序等。例如

(1)算术表达式

表示成树为

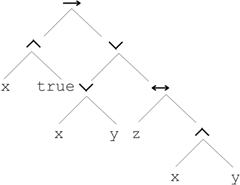
(2) 逻辑表达式：(x Ù true) ® (( x Ú y ) Ú (z « (x Ù y)))。可以由树表达为

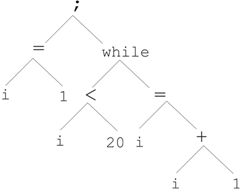
（3）程序

i =1;

while (i < 20){

i = i +1

}

可以表示为

正因为遗传编程中，以树的形式来表达基因，因此遗传编程更适于表达复杂的结构问题。其用武之地也比遗传算法广泛得多了。开始的银行寻找优良顾客就是其中一例子。

遗传编程算法的一个最为简单的例子，是尝试构造一个简单的数学函数。假设我们有一个包含输入和输出的表，如下

其背后函数实际上是x*x+x+2*y+1。现在打算来构造一个函数，来拟合上述表格中的数据。

首先构造拟合数据。定义如下函数。

def examplefun(x, y):
return x * x + x + 2 * y + 1
def constructcheckdata(count=10):
checkdata = []
for i in range(0, count):
dic = {}
x = randint(0, 10)
y = randint(0, 10)
dic['x'] = x
dic['y'] = y
dic['result'] = examplefun(x, y)
checkdata.append(dic)
return checkdata

实际上一棵树上的节点可以分成三种，分别函数，变量及常数。定义三个类来包装它们：

class funwrapper:
def __init__(self, function, childcount, name):
self.function = function
self.childcount = childcount
self.name = name
class variable:
def __init__(self, var, value=0):
self.var = var
self.value = value
self.name = str(var)
self.type = "variable"
def evaluate(self):
return self.varvalue
def setvar(self, value):
self.value = value
def display(self, indent=0):
print '%s%s' % (' '*indent, self.var)
class const:
def __init__(self, value):
self.value = value
self.name = str(value)
self.type = "constant"
def evaluate(self):
return self.value
def display(self, indent=0):
print '%s%d' % (' '*indent, self.value) 

现在可以由这些节点来构造一棵树了。

class node:
def __init__(self, type, children, funwrap, var=None, const=None):
self.type = type
self.children = children
self.funwrap = funwrap
self.variable = var
self.const = const
self.depth = self.refreshdepth()
self.value = 0
self.fitness = 0
def eval(self):
if self.type == "variable":
return self.variable.value
elif self.type == "constant":
return self.const.value
else:
for c in self.children:
result = [c.eval() for c in self.children]
return self.funwrap.function(result)
def getfitness(self, checkdata):#checkdata like {"x":1,"result":3"}
diff = 0
#set variable value
for data in checkdata:
self.setvariablevalue(data)
diff += abs(self.eval() - data["result"])
self.fitness = diff
def setvariablevalue(self, value):
if self.type == "variable":
if value.has_key(self.variable.var):
self.variable.setvar(value[self.variable.var])
else:
print "There is no value for variable:", self.variable.var
return
if self.type == "constant":
pass
if self.children:#function node
for child in self.children:
child.setvariablevalue(value)
def refreshdepth(self):
if self.type == "constant" or self.type == "variable":
return 0
else:
depth = []
for c in self.children:
depth.append(c.refreshdepth())
return max(depth) + 1
def __cmp__(self, other):
return cmp(self.fitness, other.fitness)
def display(self, indent=0):
if self.type == "function":
print ('  '*indent) + self.funwrap.name
elif self.type == "variable":
print ('  '*indent) + self.variable.name
elif self.type == "constant":
print ('  '*indent) + self.const.name
if self.children:
for c in self.children:
c.display(indent + 1)
##for draw node
def getwidth(self):
if self.type == "variable" or self.type == "constant":
return 1
else:
result = 0
for i in range(0, len(self.children)):
result += self.children[i].getwidth()
return result
def drawnode(self, draw, x, y):
if self.type == "function":
allwidth = 0
for c in self.children:
allwidth += c.getwidth()*100
left = x - allwidth / 2
#draw the function name
draw.text((x - 10, y - 10), self.funwrap.name, (0, 0, 0))
#draw the children
for c in self.children:
wide = c.getwidth()*100
draw.line((x, y, left + wide / 2, y + 100), fill=(255, 0, 0))
c.drawnode(draw, left + wide / 2, y + 100)
left = left + wide
elif self.type == "variable":
draw.text((x - 5 , y), self.variable.name, (0, 0, 0))
elif self.type == "constant":
draw.text((x - 5 , y), self.const.name, (0, 0, 0))
def drawtree(self, jpeg="tree.png"):
w = self.getwidth()*100
h = self.depth * 100 + 120
img = Image.new('RGB', (w, h), (255, 255, 255))
draw = ImageDraw.Draw(img)
self.drawnode(draw, w / 2, 20)
img.save(jpeg, 'PNG')

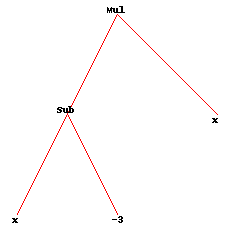
 其中计算适应度的函数getfitness（），是将变量赋值后计算所得的值，与正确的数据集的差的绝对值的和。Eval函数即为将变量赋值后，计算树的值。构造出的树如下图，可由drawtree()函数作出。 

其实这棵树的数学表达式为x*x-3x。

然后就可以由这此树来构造程序了。初始种群是随机作成的。

def _maketree(self, startdepth):
if startdepth == 0:
#make a new tree
nodepattern = 0#function
elif startdepth == self.maxdepth:
nodepattern = 1#variable or constant
else:
nodepattern = randint(0, 1)
if nodepattern == 0:
childlist = []
selectedfun = randint(0, len(self.funwraplist) - 1)
for i in range(0, self.funwraplist[selectedfun].childcount):
child = self._maketree(startdepth + 1)
childlist.append(child)
return node("function", childlist, self.funwraplist[selectedfun])
else:
if randint(0, 1) == 0:#variable
selectedvariable = randint(0, len(self.variablelist) - 1)
return node("variable", None, None, variable(self.variablelist[selectedvariable]), None)
else:
selectedconstant = randint(0, len(self.constantlist) - 1)
return node("constant", None, None, None, const(self.constantlist[selectedconstant]))

当树的深度被定义为0时，表明是从重新开始构造一棵新树。当树的深度达到最高深度时，生长的节点必须是变量型或者常数型。

当然程序不止这些。还包括对树进行变异和交叉。变异的方式的方式为，选中一个节点后，产生一棵新树来代替这个节点。当然并不是所有的节点都实施变异，只是按一个很小的概率。变异如下：

def mutate(self, tree, probchange=0.1, startdepth=0):
if random() < probchange:
return self._maketree(startdepth)
else:
result = deepcopy(tree)
if result.type == "function":
result.children = [self.mutate(c, probchange, startdepth + 1) for c in tree.children]
return result

交叉的方式为：从种群中选出两个优异者，用一棵树的某个节点代替另一棵树的节点，从而产生两棵新树。

 def crossover(self, tree1, tree2, probswap=0.8, top=1):
if random() < probswap and not top:
return deepcopy(tree2)
else:
result = deepcopy(tree1)
if tree1.type == "function" and tree2.type == "function":
result.children = [self.crossover(c, choice(tree2.children), probswap, 0)
for c in tree1.children]
return result

以上变异及交叉都涉及到从现有种群中选择一棵树。常用的选择算法有锦标赛方法，即随机选出几棵树后，按fitness选出最优的一棵树。另一种方法是轮盘赌算法。即按fitness在种群的比率而随机选择。Fitness越大的树，越有可能被选中。如下所列的轮盘赌函数。

 def roulettewheelsel(self, reverse=False):
if reverse == False:
allfitness = 0
for i in range(0, self.size):
allfitness += self.population[i].fitness
randomnum = random()*(self.size - 1)
check = 0
for i in range(0, self.size):
check += (1.0 - self.population[i].fitness / allfitness)
if check >= randomnum:
return self.population[i], i
if reverse == True:
allfitness = 0
for i in range(0, self.size):
allfitness += self.population[i].fitness
randomnum = random()
check = 0
for i in range(0, self.size):
check += self.population[i].fitness * 1.0 / allfitness
if check >= randomnum:
return self.population[i], i

其中参数reverse若为False，表明fitness越小，则这棵树表现越优异。不然，则越大越优异。在本例中，选择树来进行变异和交叉时，选择优异的树来进行，以将优良的基因带入下一代。而当变异和交叉出新的子树时，则选择较差的树，将其淘汰掉。

现在可以构造进化环境了。

def envolve(self, maxgen=100, crossrate=0.9, mutationrate=0.1):
for i in range(0, maxgen):
print "generation no.", i
child = []
for j in range(0, int(self.size * self.newbirthrate / 2)):
parent1, p1 = self.roulettewheelsel()
parent2, p2 = self.roulettewheelsel()
newchild = self.crossover(parent1, parent2)
child.append(newchild)#generate new tree
parent, p3 = self.roulettewheelsel()
newchild = self.mutate(parent, mutationrate)
child.append(newchild)
#refresh all tree's fitness
for j in range(0, int(self.size * self.newbirthrate)):
replacedtree, replacedindex = self.roulettewheelsel(reverse=True)
#replace bad tree with child
self.population[replacedindex] = child[j]
for k in range(0, self.size):
self.population[k].getfitness(self.checkdata)
self.population[k].depth=self.population[k].refreshdepth()
if self.minimaxtype == "min":
if self.population[k].fitness < self.besttree.fitness:
self.besttree = self.population[k]
elif self.minimaxtype == "max":
if self.population[k].fitness > self.besttree.fitness:
self.besttree = self.population[k]
print "best tree's fitbess..",self.besttree.fitness
self.besttree.display()
self.besttree.drawtree()  

每次按newbirthrate的比率，淘汰表现不佳的旧树，产生相应数目的新树。每次迭代完后，比较fitness，选出最佳的树。迭代的终止条件是其fitness等于零，即找到了正确的数学表达式，或者迭代次数超过了最大迭代次数。

还有其它一些细节代码，暂且按下不表。自由教程可按这里下载：http://www.gp-field-guide.org.uk/

全部代码可在这里下载：http://wp.me/pGEU6-z