如果您有疑问,可以先参考 FAQ
如果您未找到满意的答案,可以在下面留言:)
首先向大家道歉,很长时间没有来更新文章了。最近杂事太多,不好意思。
1 介绍
在上一篇文章中,我们已经看到了一个简单的关于ANN实际应用程序,这篇文章中,我将简单地介绍一下ANN的最最基础的知识以及上一篇文章中的程序原理的说明。
2 ANN的最最基础的知识
ANN算法起源于生物体的神经系统,相信大家对生物神经系统的工作方式都非常了解,这里我也就不详细介绍了,不过,为了后续说明的方便,给大家上一个截图:
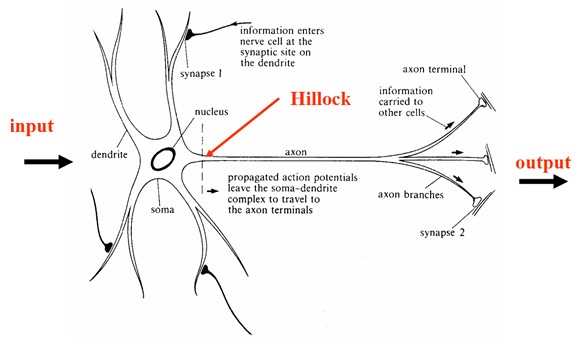
图1
根据生物神经系统的工作过程,我们可以大概理解以下这个图所要表达的含义:

图2
大家可以想象这样一种情形:寒冷的冬天,我们伸手到火炉边烤火,慢慢地,你觉得自己快要睡着了,这个时候,突然发现自己伸在火炉边的手特别烫得疼, 然后马上将手缩回去。这就是一个神经网络的工作实例,火对手产生的温度就是图2的输入层(Input),而缩手或不缩手就是图2的输出层 (Output)。但是缩手只有在手的温度达到一定的程度才发生的,比如说40度。
用图2来表示上面所说的情形:
X1 = 火对手产生的温度
w1 =火对手产生的温度的权值(对火对手产生的温度的放大或是缩小,我们让这个值为1)
激活函数(Active Function)= 如果 x1 * w1 > 40 激活(缩手),否则抑制(不缩手)
这是单输入的情况,如果有多个输入,则输出为 f(x1 * w1 + x2 * w2 + x3 * w3 …)
其中,f(x)为激活函数。
下面,我们来看2个多输入的神经网络结构图:
AND运算

其中f(x) =
If (x >= 2) return 1;
Else return 0;
阀值为2
我们可以利用这个结构图来检验一下是否正确:
X1 = 0, x2 = 0, x = x1*w1 + x2*w2 = 0 f(x) = 0;正确
X1 = 0, x2 = 1, x = x1*w1 + x2*w2 = 1 f(x) = 0;正确
X1 = 1, x2 = 0, x = x1*w1 + x2*w2 = 1 f(x) = 0;正确
X1 = 1, x2 = 1, x = x1*w1 + x2*w2 = 2 f(x) = 0;正确
OR运算

其中f(x) =
If (x >= 1) return 1;
Else return 0;
阀值为1
我们可以利用这个结构图来检验一下是否正确:
X1 = 0, x2 = 0, x = x1*w1 + x2*w2 = 0 f(x) = 0;正确
X1 = 0, x2 = 1, x = x1*w1 + x2*w2 = 1 f(x) = 1;正确
X1 = 1, x2 = 0, x = x1*w1 + x2*w2 = 1 f(x) = 1;正确
X1 = 1, x2 = 1, x = x1*w1 + x2*w2 = 2 f(x) = 1;正确
上面2个实例,就是我上篇文章中所需要建立的一个神经网络模型。
但是我们如何确定w1,w2和阀值呢?
这就需要通过神经网络来学习,从而确定w1,w2和阀值。
2 学习
拿计算AND运算的模型来说,需要2个输入1个输出是肯定的。关键就是如何确定2个输入的权值和激活函数的阀值。
为了计算激活函数的阀值,我们可以增加一个输入层,变成这个样子
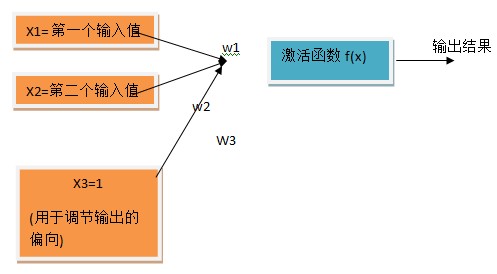
这样,我们只需让激活函数f(x)=
If (x >= 1) return 1;
Else return 0;
即可。至于阀值究竟是多少,可以让w3的值去确定。这样,原先的问题就转化成了求解w1, w2 ,w3的大小的问题了。
接下来,我们制定这样的学习规律:
W(i) = W(i) + (正确值-实际计算的值)*x(i).
通过一定次数的训练,我们就可以让 (正确值-实际计算的值)变得相当下,这样最后的结果也就稳定了,同时求出了我们需要的w1, w2 ,w3的近似值。
3实际执行过程
- 得到训练集合(合理的输入和期望的输出(如:输入x1=1,x2=1输出1))
- 随机给w1, w2,w3赋值
- 执行一定次数的训练
4 预告
在下一篇文章中,我将介绍和一个多层的神经网络,用于计算XOR(异或)操作。
5 总结
在本文中,咱们介绍了神经网络的简单最最基本的原理和上一篇文章的实例原理。
 Mikel
Mikel

